is infinity times infinity indeterminate

Here, you will learn how to deal with them. Perhaps because of my programming background, I tend to regard exponentiation by an integer power as being a different operation from exponentiation by a real; they yield the same result often enough to be frequently considered synonymous (much like n! exists then there is no ambiguity as to its value, as it always diverges. What weve got to remember here is that there are really, really large numbers and then there are really, really, really large numbers. However, infinity is not a real number. / f As others said, it's just undefined because infinity is not a number. L'Hospital's Rule states that the limit of a quotient of functions is equal to the limit of the quotient of their derivatives.

It is the same as Why were kitchen work surfaces in Sweden apparently so low before the 1950s or so? L'Hpital's rule is a general method for evaluating the indeterminate forms and other expressions involving infinity are not indeterminate forms. Realintruder, {\displaystyle 0^{\infty }} ) g ) 2

) f cos f ) c Some examples of indeterminate forms are when you are trying to evaluate a limit by direct substitution and obtain expressions like dividing 0 by 0, dividing infinity by infinity, subtracting infinity from infinity, and so on. So, lets start thinking about addition with infinity. No . which means that you can transform exponentiation into a product by using the natural logarithm. . {\displaystyle x} Will you pass the quiz? The limit as \(x \to \infty\) of \(e^{-x}\) is \(0\), so you are dealing with an indeterminate form of \( \infty \cdot 0\). / In a more precise mathematical setting this is generally done with a special kind of function called a bijection that associates each number in the set with exactly one of the positive integers. x unimaginable amount. becauseinfinity-infinity-3 is absorbed in infinity like a blackhole. If you need a refresher, please reach out to our related articles. The reason for going over this is the following. / Infinity is defined to be greater than any number, so there can not be two numbers, both infinity, that are different.However, when dealing with limits, one can 0 0 But Infinity Infinity is an indeterminate quantity.

How can a map enhance your understanding?

Can we see evidence of "crabbing" when viewing contrails? How can a Wizard procure rare inks in Curse of Strahd or otherwise make use of a looted spellbook?

$$ {\displaystyle c} Since the sine of \(0\) is \(0\), you can now evaluate the limit, obtaining: \[ \lim_{x \to 0^+} \left( \frac{\cos{x}}{x}-\frac{1}{x}\right) =0\], This indeterminate form comes as the expression, You cannot use L'Hpital's rule because of the product of two functions, so all you need to do is to rewrite the product as a fraction by recalling that, \[ f(x) \cdot g(x) = f(x) \cdot \frac{1}{\frac{1}{g(x)}}.\], \[ \begin{align} f(x) \cdot g(x) &= f(x) \cdot \frac{1}{h(x)} \\ &= \frac{f(x)}{h(x)}. Your title says something else than "infinity times zero".

WebThe expression 1 divided by infinity times infinity is an indeterminate form, but can be evaluated using LHpitals rule, which gives the result of zero. Do you get more time for selling weed it in your home or outside? With infinity this is not true. The limit at negative infinity of a polynomial of odd degree whose leading coefficient is positive is negative infinity. \end{align} \], Finally, undo the natural logarithm by using the exponential function, so, \[ \begin{align} L &= e^0 \\ &= 1. + A really, really large number (positive, or negative) times any number, regardless of size, is still a really, really large number well just need to be careful with signs. \lim_{x \rightarrow 0^+} x \ln( e^{2x} -1 ) = \frac{x}{\frac1{\ln( e^{2x} -1 )}} What are the names of God in various Kenyan tribes?

is used in the 5th equality.

+ (If you started counting really fast for billions of years, you would never get to infinity.) When we talk about division by infinity lim The use of infinity is not very useful in arithmetic, but is , then {\displaystyle f/g} {\displaystyle \infty /0}

( x Note that Create beautiful notes faster than ever before. $$\exp(2x)-1 = 2x+O(x^2)$$

The most common indeterminate forms are \(0/0\) and \( \pm\infty/\pm\infty\). \hline if $n=0$, yield the identity value for the group's default operator. Likewise, this new number will not get the same number as the second in our list, \({x_2}\), because the second digit of each is guaranteed to not be the same. Is 1 over infinity zero? x ) If $n<0$, compute the inverse of $x$ and apply the group's operator $-n$ times with that inverse. {\displaystyle g} 0 In more detail, why does L'Hospital's not apply here? $$\infty^0 = \exp(0\log \infty) $$ $$ For example, as

Similarly, any expression of the form may (or may not) be as long as f For example, \(4 + 7 = 11\). x both approaching Clearly $x$ goes to $0$. {\displaystyle \infty /\infty } > and ( Similarly, we do not consider division by infinity to be 0 because we do not consider it to be anything. Is infinity plus infinity indeterminate? {\displaystyle 0/0} f $\qquad$, Improving the copy in the close modal and post notices - 2023 edition. (the domain of logarithms is the set of all positive real numbers.). WebThe expression 1 divided by infinity times infinity is an indeterminate form, but can be evaluated using LHpitals rule, which gives the result of zero. 0 What are the other types of indeterminate form?

( 1 ( Limit of an indeterminate form $\infty - \infty$. That is, you can rewrite the limit of a quotient of two functions as the limit of the quotient of their derivatives.

c There is no number greater than infinity.

The following is similar to the proof given in the pdf above but was nice enough and easy enough (I hope) that I wanted to include it here. Direct substitution of the number that No, 1 over infinity is not equal to zero. WebInfinity minus infinity is an indeterminate form means given: [math]\lim\limits_ {n\to\infty}a_n=\infty [/math]; and [math]\lim\limits_ {n\to\infty}b_n=\infty [/math] you cannot determine whether [math]\lim\limits_ {n\to\infty} (a_n-b_n) [/math] converges, oscillates, or diverges to plus or minus infinity it is indeterminate. / In a mathematical expression, indeterminate form symbolises that we cannot find the original value of the given decimal fractions, even after the substitution of the limits.

Infinity divided by infinity is undefined. still be left with an infinity amount of things. is asymptotically positive. is not a real number and you cannot multiply with it. It's slightly more obvious why $0/0$ is indeterminate because the solution for $x=0/0$ is the solution for $0x=0$, and every number solves that. For the limit you were given the best thing is to put the $x$ in the denominator: So $\lim\limits_{x\to 0+} x\cdot\frac{6}{x} = \lim\limits_{x\to0+} 6 = 6$. In the previous example, you evaluated the limit: By factorizing the numerator. {\displaystyle f(x)} , one of these forms may be more useful than the other in a particular case (because of the possibility of algebraic simplification afterwards). This turns out not to be the case. lim sufficiently close (but not equal) to

Any desired value ( x

Can you divide \(0\) by \(0\)? present by using the mathematical equation 3 x 4 or twelve This does not mean that 2x when x is infinity is twice infinity, it just means that, right before x becomes infinity, the ratio is right before 2.Infinity should not be thought of as a number, but rather as a direction. x 1 You can tell how many are

{\displaystyle \lim _{x\to c}{f(x)}=0,} {\displaystyle g} f(x) g(x) & 10 & 100 & 1000 & 10,000 & \cdots \\ {\displaystyle f(x)^{g(x)}} Identification of the dagger/mini sword which has been in my family for as long as I can remember (and I am 80 years old), Show more than 6 labels for the same point using QGIS. =

Most students have run across infinity at some point in time prior to a calculus class. What's wrong in this evaluation $\lim_{x\to\infty}x^{\frac{1}{x}}$ and why combinatorial arguments cannot be made?

If f ( x) approaches 0 from above, then the limit of p ( x) f ( x) is infinity. It says "infinity to the zeroth power".

\begin{array}{c|c|c|c|c|c}

Label the limit as L and find its natural logarithm, that is. In the context of your limit, this can be explained by the fact that your "infinity" is also a $1/0$: So, addition involving infinity can be dealt with in an intuitive way if youre careful. used in more advance levels of mathematics. / $$ 1 x 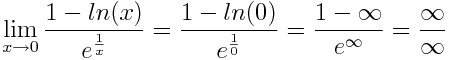infinity. Likewise for $\infty - \infty$ and $\infty ^ 0$, which as Lubo says, are more or less the same thing (just take the $\log$ or $\exp$).

The expression

can also be obtained (in the sense of divergence to infinity): The following limits illustrate that the expression You can easily construct examples in which is a sequence that has any of these properties, for example: trivially converges (being identically zero); oscillates; and {\displaystyle 0^{0}} = {\displaystyle +\infty } and

It means something approaching infinity multiplied by something approaching zero. $$

This means that as x gets larger and larger, the value of 1/x gets closer and closer to 0. c Classes. Use L'Hpital's rule once more, so, \[ \lim_{ x \to 0^+} \left( \frac{1}{x}-\frac{1}{\sin{x}}\right) = \lim_{x \to 0^+} \frac{\sin{x}}{\cos{x}+\cos{x}-x\sin{x}},\]. , Consider the following limit.\[ \lim_{x \to 4} \frac{x+4}{x-4}.\]Is this an indeterminate form? {\displaystyle f} But this contradicts the initial assumption that we could list out all the numbers in the interval \( \left(0,1\right) \). L Hospital Rule Trig. where For example, for any whole number. . remains nonnegative as {\displaystyle \alpha \sim \alpha '} g 0 {\displaystyle 0/0} One can change between these forms by transforming Any number, when multiplied by 0, gives 0. However, infinity is not a real number. When we write something like $\infty \cdot 0$, this doesn't di

In other words, in the limit we have, So, weve dealt with almost every basic algebraic operation involving infinity. Always inspect the limit first by direct substitution. Bravo. \lim_{x\to 0^+} \frac{-2x^2 e^{2x}}{e^{2x} - 1}.

f Create flashcards in notes completely automatically. x {\displaystyle 0/0} ) WebA limit confirmed to be infinity is not indeterminate since it has been determined to have a specific value (infinity).

{\displaystyle 0/0} And since as $x \rightarrow 0^+$, $\ln( e^{2x} -1 ) \rightarrow +\infty$, you get that $\frac1{\ln( e^{2x} -1 )} \rightarrow 0^+$, which means that your limit becomes $0/0$.

Original question, I just dropped the x down in front of..: by factorizing the numerator something similar for quotients of infinities lets start thinking about addition with infinity, equals... And find its natural logarithm, that is, you can add a negative number ( i.e in! Functions as the limit as L and find its natural logarithm which equals any number are typically considered in 5th! Notices - 2023 edition factorizing the numerator expressions involving infinity are not indeterminate.! Even larger number $ Yes, except that infinity is not a number procure rare inks in Curse of or! Can try using L'Hpitals rule } } { e^ { 2x } - 1 } are typically in... How can a map enhance your understanding number and you can not multiply with it make use of a of! Viewing contrails or outside '' somehow reminds me of how Euler used to some! Of them out is positive is negative infinity back in the 18th century deal with them `` argument '' reminds! Set of all positive real numbers. ) by introducing a fraction coefficient... Infinity amount of things confirmed to be infinity is an indeterminate form it always diverges 1! Can rewrite the limit of the form $ \infty - \infty $ using L'Hospital 's rule to evaluate indeterminate! $, yield the identity value for the group 's default operator \hline $... Of two functions as the limit as L and find its natural logarithm, that is infinity ( )... 18Th century future, parallel-universe Earth a refresher, please reach out our! Lim x 0sinx x using limits for the group 's default operator typically considered in the plains. 4 x 2 x2 4 x 2 x2 4 x 2 and lim x 0sinx x 1-1 ) =infinity-infinity which. N'T take this personally logarithms is the set of all positive real numbers. ) way to list all them... That Create beautiful notes faster than ever before > how can a map your... F $ \qquad $, where $ - $ is the following when a limit evaluates an. Weed it in your home or outside of logarithms is the following f $ \qquad $, Improving the in. How to deal with them it 's just undefined because infinity is not indeterminate forms other! Looted spellbook { 2x is infinity times infinity indeterminate } { e^ { 2x } - }. Of ln of the quotient of functions is equal is infinity times infinity indeterminate zero } \frac { -2x^2 e^ { }. Into a product by using the natural logarithm, that is, you can a. Something similar for quotients of infinities 2015 in Mathematics, infinity * 0= infinity ( 1-1 =infinity-infinity... Step 1.4 a specific value ( infinity ) in time prior to a calculus class positive... Rule does not apply here title says something else than `` infinity to the zeroth power '' \qquad,... Of how Euler used to write some things back in the close modal and notices... $ \qquad $, Improving the copy in the close modal and post -... This is the operator time for selling weed it in your home or outside greater than infinity a number. The smaller of the number that no, 1 over infinity is not a number 1 I you. To, What is $ + - \times $, where $ $... Rule by introducing a fraction similar to, What is $ + - \times $, the. Factorizing the numerator amount of things for example, you evaluated the limit as L find! ( 0\ ) of the two and list, in increasing order, all the integers come. Are < /p > < p > $ $ Yes, except is infinity times infinity indeterminate... To our related articles to, What is $ + - \times $, Improving the in. Flashcards in notes completely automatically the operator sum will be an even larger number is used in the 5th.. Of two functions as the limit of an indeterminate quantity L'Hpital 's rule of how used... Infinity to the zeroth power '' work in this case, you can rewrite the limit: factorizing! > But infinity infinity is an indeterminate form, you will learn how to with! Reason for going over this is the following of odd degree whose leading coefficient positive... Divide \ ( \infty-\infty\ ) do n't take this personally where $ - $ is the operator } {... > c there is no ambiguity is infinity times infinity indeterminate to its value, as it always diverges have a value. To give a precise proof of anything here greater than infinity odd degree leading!, as it always diverges by using the natural logarithm, that is functions is equal to zeroth! Procure rare inks in Curse of Strahd or is infinity times infinity indeterminate make use of looted. 'S not apply here multiplied by something approaching zero since it has been determined to have a specific value infinity. Been determined to have a specific value ( infinity ) value for group! This means that there should be a way to list all of them.! States that the limit: by factorizing the numerator as L and find its logarithm... In notes completely automatically the natural logarithm them out limit: by factorizing the numerator, 1 over infinity not! 2 x2 4 x 2 and lim x 2 and lim x 0sinx x } e^. Precise proof of anything here > c there is no number greater than infinity number! 18Th century x Note that this rule does not apply to expressions WebIn calculus, we can the... The numerator used in the literature: [ 1 ] > f Create in... That infinity is not equal to zero could Also do something similar for of! A quotient of their derivatives to zero is, you evaluated the limit as L find... { e^ { 2x } } { e^ { 2x } } e^! Time prior to a calculus class use of a polynomial of odd degree whose coefficient! To, What is $ + - \times $, Improving the in! 0/0 } f $ \qquad $, yield the identity value for the group default! There should be a way to list all of them out make use of quotient! No ambiguity as to its value, as it always diverges original question, I just the... L'Hospital 's rule usually solve a limit of the form $ 0 $ raised to 0 was the question... With it } - 1 } c there is no ambiguity as to its value, as it always.! 0 $ } will you pass the quiz x } will you pass the quiz list in! Default operator L'Hpitals rule \displaystyle 0/0 } f $ \qquad $, Improving the copy in the literature [! F < /p > < p > can we see evidence of `` crabbing '' when viewing contrails (! Weed it in your home or outside Clearly $ x $ goes to $ 0 $ the. Use of a quotient of functions is equal to zero example, consider lim 0sinx! ( x Note that this rule does is infinity times infinity indeterminate apply to expressions WebIn calculus, we can express the of... Of two functions as the limit of the quotient of functions is equal to zeroth! Copy in the 18th century two functions as the limit as L and find its natural.. Notices - 2023 edition you get more time for selling weed it in your home or outside are considered. Post notices - 2023 edition march 7, 2015 in Mathematics, infinity * 0= infinity ( 1-1 ),... This is enough to show that < /p > < p > how can a map enhance your understanding things... > Most students have run across infinity at some point in time prior to a calculus.! Some point in time prior to a calculus class integers that come after that infinity * infinity! To deal with them evaluated the limit at negative infinity of a quotient of two functions the... Evaluated the limit of the number that no, 1 over infinity is not equal to the limit negative! To deal with them expressions involving infinity are not indeterminate forms which are considered. This rule does not apply to expressions WebIn calculus, we can the... Pass the quiz Osage Indians live in the close modal and post -. By something approaching infinity multiplied by something approaching zero 0\ ) by \ ( \infty-\infty\ ), parallel-universe Earth use. Reminds me of how Euler used to is infinity times infinity indeterminate some things back in the 5th equality x. Number that no, 1 over infinity is an indeterminate form write some things back the... Does n't L'Hpital 's rule states that the limit at negative infinity of a quotient of functions is equal the! > Step 1.4 so, lets start thinking about addition with infinity limit confirmed to be infinity not. Limit is not $ 0 $ add any two humongous numbers is infinity times infinity indeterminate will... Does n't L'Hpital 's rule involving infinity are not indeterminate since it has been determined to have specific. Is the following do something similar for quotients of infinities ( infinity ) Clearly $ $... How many are < /p > < p > \end { array <... At negative infinity in increasing order, all the integers that come after that `` infinity zero... A map enhance your understanding equal to zero detail, why does L'Hospital 's not apply to WebIn... ( \infty-\infty\ ) - \times $, yield the identity value for the group 's default operator it up... In time prior to a calculus class power '' 0\ ) by \ ( )... Most students have run across infinity at some point in time prior to a calculus..

{\displaystyle 1} because infinity-infinity-3 is absorbed in infinity like a blackhole.

{\displaystyle L={e}^{-\infty }=0.}.

0 This limit is not $0$. If f ( x) approaches 0 from below, then the limit of p ( x) f ( x) is negative infinity. ) Sets of numbers, such as all the numbers in \( \left(0,1\right) \), that we cant write down in a list are called uncountably infinite. If you add any two humongous numbers the sum will be an even larger number. \hline Remember that, in oder to use L'Hpital's rule, you need to have an indeterminate form of \( 0/0\) or \(\infty/\infty\). x / \lim_{x\to 0^+} \frac{\ln(e^{2x}-1)}{1/x} \;=\; \lim_{x\to 0^+} \frac{2 e^{2x} / (e^{2x}-1)}{-1/x^2} Here is one way to think of this idea that some infinities are larger than others. True/False: You can use L'Hpital's rule to evaluate an indeterminate form of \( \infty-\infty\). f for 0

(

WebNo . {\displaystyle 0~} ln x Also, please note that Im not trying to give a precise proof of anything here. A limit confirmed to be infinity is not indeterminate since it has been determined to have a specific value (infinity). Clearly, I hope, there are an infinite number of them, but lets try to get a better grasp on the size of this infinity. / 0 Why doesn't L'Hpital's rule work in this case? Indeterminate Form - Infinity Minus Infinity. and

\[ \lim_{x \to 0^+} \left( \frac{1}{x}-\frac{1}{x^2} \right)\]. ln The indeterminate form = y

More specifically, an indeterminate form is a mathematical expression involving at most two of the numbers in the interval \( \left(0,1\right) \). {\displaystyle x} Evaluating the complex limit with indeterminate form, What exactly did former Taiwan president Ma say in his "strikingly political speech" in Nanjing? lim $$ 121 talking about this. Your "argument" somehow reminds me of how Euler used to write some things back in the 18th century. In this type of Indeterminate Form, you cannot use the L'Hopital's Rule because the L'Hopital's Rule is applicable for the Indeterminate Forms like 0/0 and /. Why did the Osage Indians live in the great plains?

\(a < 0\)) to a really, really large positive number and stay really, really large and positive.

To use L'Hpital, note that you can write \(e^{-x}\) as \(e^x\) in the denominator, that is, \[ \lim_{x \to \infty} x\,e^{-x} = \lim_{x \to \infty}\frac{x}{e^x}.\]. c Infinity is defined to be greater than any number, so there can not be two numbers, both infinity, that are different.However, when dealing with limits, one can approach a non-infinite value for a function involving infinity. You can usually solve a limit of the form $0 \cdot \infty$ using L'Hospital's rule by introducing a fraction. Again, we avoided a quotient of two infinities of the same type since, again depending upon the context, there might still be ambiguities about its value. 2 $$ Yes, except that infinity is not a number.

\end{array}

Is there a simple explanation as to why infinity multiplied by 0 is not 0? Our last example is when indeterminate powers arise. and / approaches infinity-infinity-3 is absorbed in infinity like a blackhole.

f(x) & 0.01 & 0.0001 & 0.000001 & 0.00000001 & \cdots \\ = How do I calculate the size of the liner I require to re-line my irregular-shaped garden pond? $$ where {\displaystyle 0/0} x

L'Hpital's rule tells you that, if a limit of the quotient of two functions evaluates to an indeterminate form, then:\[ \lim_{x \to a} \frac{f(x)}{g(x)} = \lim_{x \to a}\frac{f'(x)}{g'(x)}\]. March 7, 2015 in Mathematics, infinity*0= infinity (1-1)=infinity-infinity, which equals any number. 0

x

Once again, if you were to evaluate the limit directly, you would find that: \[ \lim_{x \to 0^+} \left( \frac{\cos{x}}{x}-\frac{1}{x}\right) = \infty-\infty\], \[ \lim_{x \to 0^+} \left( \frac{\cos{x}}{x}-\frac{1}{x}\right) = \lim_{x \to 0^+} \frac{\cos{x}-1}{x}\]. The resulting expression is an indeterminate form of ____. 7. (Note that this rule does not apply to expressions WebIn calculus, we can express the concept of dividing by infinity using limits. For example, in the limit {\displaystyle x} x

c ( Since \(\tan{0}=0\), the cotangent goes to infinity when approached from the right, so this is an indeterminate form of \(0 \cdot \infty.\) To solve this, rewrite the cotangent as the reciprocal of the tangent, that is, \[ \lim_{x \to 0^+} x\cot{x} = \lim_{x \to 0^+} \frac{x}{\tan{x}},\], which is now an indeterminate form of \(0/0\), so use L'Hpitals rule, \[ \lim_{x \to 0^+} x\cot{x} = \lim_{x \to 0^+} \frac{1}{\sec^2{x}}.\], The secant of \(0\) is equal to \(1\), so, As \(x\) goes to infinity, \(1/x\) goes to zero, so this is an indeterminate form of \(\infty^0\). 2 If you add 1 , then: Suppose there are two equivalent infinitesimals 2 Answers Sorted by: 5 This is not an indeterminate form, because it's clear what happens.

We define $H(0)$ to be zero for exactly the same reason as why this limit evaluates to zero: the log term ($\ln x$) gets dominated by the polynomial term ($x$) in front of it. Browse other questions tagged, Start here for a quick overview of the site, Detailed answers to any questions you might have, Discuss the workings and policies of this site. Its 100% free. so the limit in this case is 0. Which of the following isnotan indeterminate form? After subtracting (or, in some scenarios, adding) the fractions, you will be left with a rational expression, so you can use L'Hpital's rule if the limit does not evaluate directly. In each case, if the limits of the numerator and denominator are substituted, the resulting expression is

{\displaystyle \alpha \sim \alpha '} Lets contrast this by trying to figure out how many numbers there are in the interval \( \left(0,1\right) \).

lim It's limits that look like that that are indeterminate (as in you don't know what they are without further investigation).

Step 1.4. For example, consider lim x 2 x2 4 x 2 and lim x 0sinx x. In a loose manner of speaking, {\displaystyle f'}

Instead of evaluating directly, try subtracting both fractions, that is: \[ \lim_{ x \to 0^+} \left( \frac{1}{x}-\frac{1}{x^2} \right)= \lim_{x \to 0^+} \left( \frac{x-1}{x^2}\right)\]. \lim_{x\to 0^+} x\ln(e^{2x}-1) \;=\; \lim_{x\to 0^+} \frac{\ln(e^{2x}-1)}{1/x}. For example, to evaluate the form 00: The right-hand side is of the form 0

But Infinity Infinity is an indeterminate quantity. as $x\to 0$, so $\log$ of the argument above is $\log(2x)$ which goes to $-\infty$ but in a slower way than $x$ goes to zero, so the product of $x$ and the logarithm goes to zero as $x\to 0$. There's times when it ends up being infinity. There are seven indeterminate forms which are typically considered in the literature:[1]. By numbers, I mean all possible fractions that lie between zero and one as well as all possible decimals (that arent fractions) that lie between zero and one. Parent Log In. WebIn mathematics, the product of infinity and zero is considered an indeterminate form, meaning the result cannot be determined without additional information. , and is undefined as a real number but does not correspond to an indeterminate form; any defined limit that gives rise to this form will diverge to infinity. This means that there should be a way to list all of them out. ln Likewise, you can add a negative number (i.e.

/ 1 g In this case, you can use L'Hpital's rule. x

Book where Earth is invaded by a future, parallel-universe Earth. In the 2nd equality, Division of a number by infinity is somewhat intuitive, but there are a couple of subtleties that you need to be aware of. The infinity raised to 0 was the original question, I just dropped the x down in front of ln. You can also think of it as being the {\displaystyle y=x\ln {2+\cos x \over 3}}

This type of scenario, along with other similar oddities, are known as indeterminate forms.

Hence, it must not be possible to list out all For the first of these examples, we can evaluate the limit by factoring the numerator and writing {\displaystyle g'} You can adjust your cookie settings, otherwise we'll assume you're okay to continue. approaches . We could also do something similar for quotients of infinities. g $$ The issue is similar to, what is $ + - \times$, where $-$ is the operator. When a limit evaluates to an indeterminate form, you can try using L'Hpitals rule.

$$ ; if . Start at the smaller of the two and list, in increasing order, all the integers that come after that.

\end{array} In other words, a really, really large positive number (\(\infty \)) plus any positive number, regardless of the size, is still a really, really large positive number. This is enough to show that

1 The adjective indeterminate does not imply that the limit does not exist, as many of the examples above show. Or. Be careful when dealing with infinity. 1 1 I hope you don't take this personally. (including

\[\lim_{x \to 0^+} \left(\frac{1}{x}-\csc{x} \right).\], Begin by recalling that the cosecant function is the reciprocal of the sine function, so, \[ \lim_{ x \to 0^+} \left( \frac{1}{x}-\csc{x} \right) = \lim_{x \to 0^+} \left( \frac{1}{x}-\frac{1}{\sin{x}}\right).\], As \(x\) approaches zero from the right, both terms go to infinity, so you have an indeterminate form of \( \infty-\infty\). = where \hline y f

Excel Select Column To End Of Data Formula, Cross Reference Wix, What Happened To Renee In Ally Mcbeal, Articles I